●数理解析学2
| 担 当 者 |
単 位 数 |
配当年次 |
学 期 |
曜 日 |
時 限 |
| 中村 孔一 講師 |
2 |
1 |
第2学期 |
木 |
2 |

-
「数理解析学1」で学習した1変数関数の微積分の知識を基にして、多変数の関数の微積分を学ぶ。多変数関数の微積分は、力学、電磁気学、熱力学、統計力学、量子力学などの物理学の基礎理論を学ぶために不可欠な言葉である。いわば、仏文科の学生のフランス語、英文科の学生の英語に対応するものであり、多変数関数の微積分を自由に読み書き話せることは、物理科学生の必須条件である。
-
| 1 | なぜ多変数関数の微積分が物理学に必要なのか |
| 2 | 偏微分と偏微分方程式 波動方程式の例 |
| 3 | 関数値の変化 全微分 |
| 4 | 条件付の極大・極小問題 |
| 5 | 曲面の性質 |
| 6 | 多変数関数のテーラー展開 |
| 7 | 偏微分の変数変換 |
| 8 | 2次元と3次元のラプラシアンの極座標表示 |
| 9 | 多重積分とは |
| 10 | 逐次積分 積分順序の交換 |
| 11 | 積分変数の変換 |
| 12 | 変数変換のつづき |
| 13 | 立体の体積と表面積 |
-
できる限りていねいに説明するつもりであるが、時間の制約から多くの具体例に触れる余裕はない。そのかわりに、練習問題を配布する。各自の自習を期待する。質問、コメントは大小にかかわらず歓迎する。
-
第2学期(学年末試験)
学年末に試験を行い、その結果によって評価する。
-
江沢洋『微分積分の基礎と応用』(新数理ライブラリM2)サイエンス社
前期の数理解析1の教科書と同じです。
-
杉浦光夫『解析入門
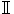 』(基礎数学3)東京大学出版会
』(基礎数学3)東京大学出版会
数学者の書いた本格的な入門書。数学的な厳密さが気になる人には格好の参考書。
![]()
![]()
![]()
![]()
![]()
![]()
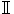 』(基礎数学3)東京大学出版会
』(基礎数学3)東京大学出版会