●微分積分I

微分積分学は解析学の基礎であり、同時に数学全般のみならず、自然科学・工学に欠かせない道具である。さらに、数学科での微分積分は、極限とか連続性とか「無限」にまつわる理論（論理）に始めて直面する場であり、そこでの修練が数学科で数学的な考え方を広く学ぶための基礎となることが期待されている。この講義と演習では、微分積分のこの性格を踏まえて、基礎（論理）と応用（計算）をバランスよく学ぶことをモットーとするが、基礎的理解を徹底することにやや重点を置くことになろう。
微分積分１演習とセットで履修することを必要とする。どちらか一方だけの単位取得は認めない。

以下は重要項目であって、１回毎の講義内容ではない。 １　実数の連続性の公理 ２　上限・下限 ３　数列の極限 ４　数列の極限と連続性の諸相 ５　無限級数 ６　連続関数：写像、関数、関数の極限、１ ７　関数の極限、２；連続関数、 ８　連続関数、２；一様連続 ９　関数列の収束、一様収束 10　微分積分の基礎理論：導関数と原始関数 11　連続関数の定積分、 12　リーマン積分、 13　広義積分 14　微分積分の展開、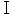：高階導関数と凸関数 15　微分積分の展開、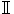：一様収束と微分積分 16　べき級数 17　テイラー展開 18　不定積分の計算法、

板書による。普通の講義形式

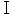数学科の学生に対しては、微分積分・同演習をセットとして成績評価する。一方だけ単位取得は認めない。

評価は次の（a）（b）を総合して行う。（a）学期の中間・期末試験、（b）演習への出席および問題回答の実績評価

占部実他著『理工科系一般教育・微分積分教科書』共立出版

黒田成俊著『微分積分』共立出版
高木貞治著『解析概論』岩波書店