● ○微分積分III　数２年

「微分積分」に引き続き微分積分について講義する。前半は、独立変数が多数ある場合の微分積分に重点を置く。後半はベクトル解析について講義する。

１	以下の内容は、重要項目であって、１回毎の講義内容ではない。
２	多変数関数の極限値、連続性
３	偏微分法
４	全微分
５	合成関数の微分法、連鎖律
６	高い階数の偏導関数
７	テイラーの定理
８	多変数関数の極大、極小
９	陰関数定理
10	ラグランジュ乗数法
11	簡単な偏微分方程式
12	多重積分の概念
13	累次積分
14	変数変換とヤコービ行列式
15	広義積分
16	＜ベクトル解析＞
17	ベクトル場と外積、偏微分
18	曲線の色々
19	色々な曲面
20	線積分
21	面積分
22	ガウス-グリーンの定理、ベクトル場の発散
23	ストークスの定理

板書による。

第1学期 （学期末試験） ：試験を実施する

中間試験を行うことがある。成績は「微分積分演習」とあわせて総合的に評価する。

吹田信之、新保経彦『理工系の微分積分学』学術図書出版社、2007年、ISBN:9784873611198

黒田成俊『微分積分』（共立講座　２１世紀の数学）共立出版、2002年
小林昭七『続　微分積分読本−多変数』裳華房、2001年
高木貞治『解析概論』改訂第三版、岩波書店、1983年
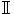藤田宏『大学での微分積分』岩波書店、2004年