● 経営科学特殊研究Ⅲ
―ブラック＝ショールズ方程式の導出――

ブラック＝ショールズ方程式は昔，MBAコースで学んだが，結局理解できなかった，というかたのために，ゆっくりと分かりやすくブラック=ショールズ方程式の導出を説明します．もちろん，初めて学ぶという人も対象です．微分，偏微分，指数関数，対数関数，期待値，分散，正規分布などの数学の考え方をビジュアルに解説します．ビジュアルな教材とは，3次元グラフィクス，スライダー，アニメーションなどを使い，コンピュータ画面上でグラフィクスを操作しながら，数式の意味するところを分かり易く理解できるようにした教材です．平均値，標準偏差の値をスライダーで動かすことで，つまり，身体を動かすことで，正規分布の性質が真から納得できるようになります．また，講義では，中心極限定理，正規分布の確率密度関数，ブラウン運動，伊藤のレンマなどの用語を解説します．数学から離れていた人を対象として，確率，統計を基礎からグラフィクスを使って分かりやすく実践的に教えますので，安心して履修してください．数学に詳しい人にも，本講座の中心極限定理のグラフィクスによる教え方は面白い，と好評です．シミュレーションを見れば，さらに詳しく納得できます．ですからブラックショールズには興味がなくても，統計をしっかり再勉強したい人にも適したクラスです．
大学院のD/M科目である．Mコースの目標は，個々の定理等を理解し，導出過程の全様を理解することです．Dコースの目標はさらに進め，定理の取捨選択を行い，自分でモデルを構築するスキルの養成です．
金融工学のモデル構築方法は他分野のかたにも役立つ知識です．ともかく，楽しい，分かる，しかも実践的なクラスです．

株価の変動


2次有限変分


対数正規分布

1	オリエンテーション：　ゴールの公式までの演繹推論の概説「ブラックショールズの公式とはオプションの利潤の期待値の式」
2	確率の考え方，余事象の確率，順列と組合せ，独立試行の期待値，条件付き確率（ベイズの定理）
3	偶然の法則と確率分布，正規分布，母平均と標本平均，統計的推測，中心極限定理，95％信頼区間は1.96σ
4	正規分布の確率密度関数，指数関数と対数関数の微分
5	公式導出に必要な数学公式のレビュー
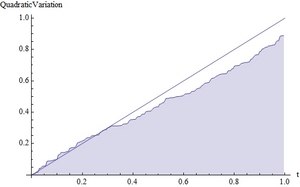
6	ブラウン運動，伊藤のレンマ，2次有限変分
7	ランダムウォークの時間の連続化(確率論の専門家をゲスト講師に呼ぶ予定）
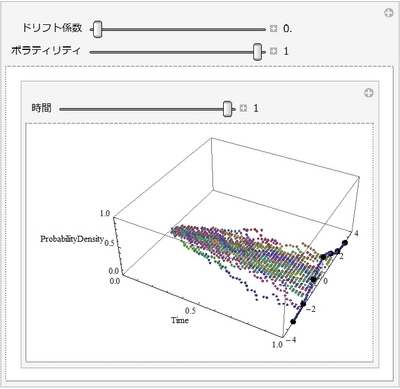
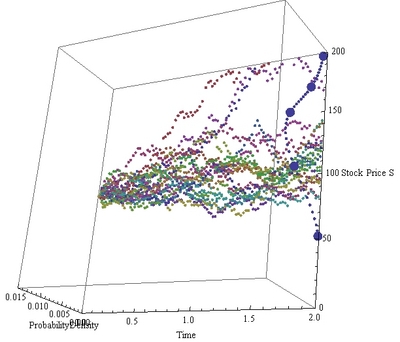
8	連続型確率変数の期待値，株価の確率密度関数，対数正規分布
9	ブラックショールズ公式を求める2次式の平方完成，公式導出
10	オプションの現在価値，連続複利法，現在価値と将来価値
11	ブラックショールズ公式のまとめ：その演繹推論過程のレビュー
12	時系列分析，自己相関の検定
13	〃
14	ベキ乗則，正規分布とベキ分布，ベキ乗関数のグラフ，ベキ乗と指数関数の区別，スケールの不変性
15	総復習

金融の現場で活躍している人，将来金融の分野で活躍したい人の数学力，論理力を伸ばすための講義です．少人数の面授による演習です．日本の数学は，目の前の数学問題を急いで解く，という科目になっていますが，このクラスは異なります．先生と対話しながらグラフィクスを見ながら，数学をゆっくり考え理解していきます．テキストは独自にこの科目用に作成したものを使います．また，すべての項目に教員が作成したグラフィクスが付きます．家でも使えます．今までの数学とは違う数学を体験してみたい人，数学ができるようになりたい人，金融数学のセンスを身に着けたい人，いらしてください．

昨年度の本講義では，伊藤のレンマの2次変分有限などの数学の証明はスキップしました．今年も「難しい証明はスキップして，本筋を掴む」「シミュレーションで見て，内容を理解する」という方針に変わりはありません．しかし，きちんとしたブラウン運動の定義の講義を確率論の専門家から一度は聴いておきたい，です．そこで，今年も，ゲスト講師をお呼びして，ランダムウォークの時間の連続化について，分かりやすく説明して頂く予定です．伊藤積分の数学的内容は大変難しく，本講義の範囲を逸脱しますので，経営学科むきに分かりやすくお話しして頂きます．難しくないので安心してください．大学院の講義で，少人数ですので，全員がブラック＝ショールズ方程式を分かった気分になるまで，懇切丁寧に責任をもって教えます．本講義は，社会人の科目等履修生を想定しています．人によって，分からない部分が違いますが，今年も，分かるまで繰り返し教えます．昨年度の受講者は，全員分かった気分になれました．How2SolveItシステムにより，講義の中でコンピュータ・ビデオを補助教材として用います．授業の理解が十分でなかった時，欠席した時も自分自身の理解のレベルに沿って，復習や授業の補足が出来ます．

レポート：50％

平常点（出席、クラス参加、グループ作業の成果等）：50％

忙しい社会人(金融関連等）が多いので，仕事の都合も考慮します．Dコースとして履修する学生に対しては，別途，モデル構築に関する課題レポートを追加で出します．

白田由香利，橋本隆子，市川収，鈴木桜子『大学生のための役に立つ数学』、共立出版、2014年

白田の公開数学教材サイト　(1)数学教材 説明ビデオとグラフィクス教材　(http://www-cc.gakushuin.ac.jp/~20010570/ABC/) (2)英語　Central Limit Theorem　VIDEO　(http://www-cc.gakushuin.ac.jp/~20010570/mathABC/)　(3)関連論文：学習院大学経済論集　論文「演繹推論法によるブラック＝ショールズ方程式の導出」，「ブラック＝ショールズ方程式に関するシミュレーションとグラフィクスによる考察」http://www.gakushuin.ac.jp/univ/eco/gakkai/pdf_files/keizai_ronsyuu/　で公開．

白田由香利『悩める学生のための経済経営数学入門』、共立出版、2009年

白田由香利，橋本隆子，飯高茂『感じて理解する数学入門(e-Book)』、オライリー・ジャパン、2012年

履修者数制限あり。
第1回目の授業に必ず出席のこと｡

---